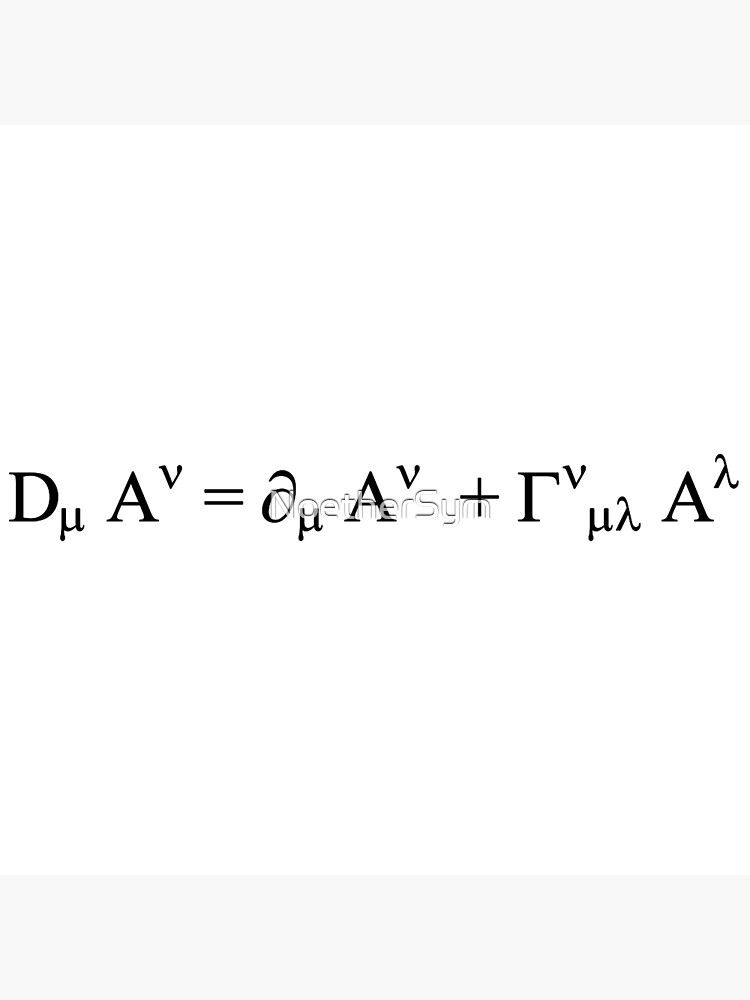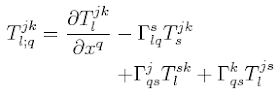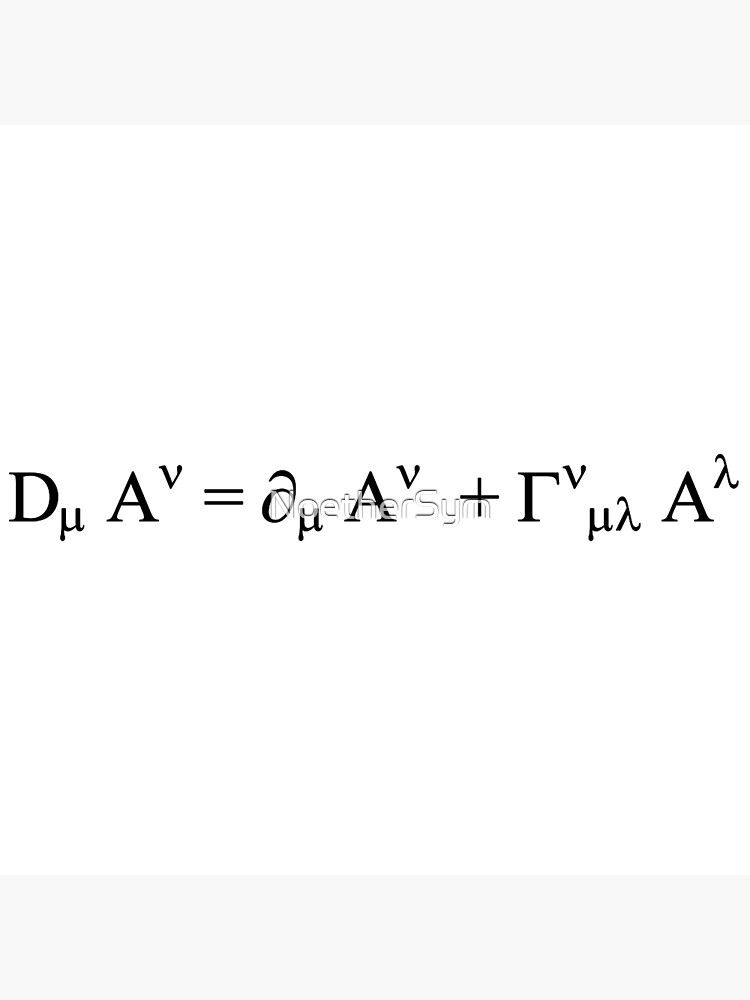Derivada covariante gauge

La derivada covariante gauge es una generalización de la derivada covariante utilizada en relatividad general. Si una teoría tiene simetrías gauge, significa que algunas de las propiedades físicas de ciertas ecuaciones no se modifican bajo aquellas transformaciones. Así mismo, la derivada covariante gauge es la derivada normal modificada de tal manera que se comporte como un verdadero operador vectorial, de modo que las ecuaciones escritas utilizando la derivada covariante preservan sus propiedades físicas bajo transformaciones gauge.

Dinámica de fluidos

En dinámica de fluidos, la derivada covariante gauge de un fluido se define como

${\displaystyle \nabla _{t}\mathbf {v} :=\partial _{t}\mathbf {v} (\mathbf {v} \cdot \nabla )\mathbf {v} }$

donde ${\displaystyle \mathbf {v} }$ es el campo vectorial de la velocidad de un fluido.

Teoría gauge

En teoría gauge, que estudia una clase particular de campos que tienen de importancia en la teoría de campos cuánticos, la derivada covariante en acoplamiento mínimo se define como

${\displaystyle D_{\mu }:=\partial _{\mu }-ieA_{\mu }}$

donde ${\displaystyle A_{\mu }}$ es el cuadrivector de potencial electromagnético.

(Nota que esto es válido para una signatura ${\displaystyle (-, , , )}$ en la métrica de Minkowski, la que se emplea en este artículo. Para ${\displaystyle ( ,-,-,-)}$ el menos pasa a ser un más.)

Construcción de la derivada covariante a través del requisito de covarianza gauge

Considerar una transformación gauge genérica (posiblemente no-abeliana) dada por

${\displaystyle \phi (x)\rightarrow U(x)\phi (x)\equiv e^{i\alpha (x)}\phi (x),}$

${\displaystyle \phi ^{\dagger }(x)\rightarrow \phi ^{\dagger }(x)U^{\dagger }(x)\equiv \phi ^{\dagger }(x)e^{-i\alpha (x)},\qquad U^{\dagger }=U^{-1}.}$

donde ${\displaystyle \alpha (x)}$ es un elemento del álgebra de Lie asociada con el grupo de Lie de transformaciones, y se puede expresar en términos de los generadores como ${\displaystyle \alpha (x)=\alpha ^{a}(x)t^{a}}$.

La derivada parcial ${\displaystyle \partial _{\mu }}$ transforma consiguientemente como

${\displaystyle \partial _{\mu }\phi (x)\rightarrow U(x)\partial _{\mu }\phi (x) (\partial _{\mu }U)\phi (x)\equiv e^{i\alpha (x)}\partial _{\mu }\phi (x) i(\partial _{\mu }\alpha )e^{i\alpha (x)}\phi (x)}$

y por tanto un término cinético de la forma ${\displaystyle \phi ^{\dagger }\partial _{\mu }\phi }$ no es invariante bajo esta transformación.

Podemos introducir la derivada covariante ${\displaystyle D_{\mu }}$ en este contexto como generalización de la derivada parcial ${\displaystyle \partial _{\mu }}$ que transforma covariantemente bajo la transformación gauge, esto es, un objeto que satisface

${\displaystyle D_{\mu }\phi (x)\rightarrow D'_{\mu }\phi '(x)=U(x)D_{\mu }\phi (x),}$

que en términos de operadores toma la forma

${\displaystyle D'_{\mu }=U(x)D_{\mu }U^{\dagger }(x).}$

Así pues calculamos (omitiendo las dependencias explícitas en ${\displaystyle x}$ por brevedad)

${\displaystyle D_{\mu }\phi \rightarrow D'_{\mu }U\phi =UD_{\mu }\phi (\delta D_{\mu }U [D_{\mu },U])\phi }$,

donde

${\displaystyle D_{\mu }\rightarrow D'_{\mu }\equiv D_{\mu } \delta D_{\mu },}$

${\displaystyle A_{\mu }\rightarrow A'_{\mu }=A_{\mu } \delta A_{\mu }.}$

El requisito para que ${\displaystyle D_{\mu }}$ transforme covariantemente se traduce ahora en la condición

${\displaystyle (\delta D_{\mu }U [D_{\mu },U])\phi =0.}$

Para obtener una expresión explícita hacemos el Ansatz

${\displaystyle D_{\mu }=\partial _{\mu }-igA_{\mu },}$

de donde se sigue que

${\displaystyle \delta D_{\mu }\equiv -ig\delta A_{\mu }}$

y

${\displaystyle \delta A_{\mu }=[U,A_{\mu }]U^{\dagger }-{\frac {i}{g}}[\partial _{\mu },U]U^{\dagger }}$

que ${\displaystyle U(x)=1 i\alpha (x) {\mathcal {O}}(\alpha ^{2})}$ es de la forma

${\displaystyle \delta A_{\mu }={\frac {1}{g}}([\partial _{\mu },\alpha ]-ig[A_{\mu },\alpha ]) {\mathcal {O}}(\alpha ^{2})={\frac {1}{g}}[D_{\mu },\alpha ] {\mathcal {O}}(\alpha ^{2})}$

Así que hemos encontrado un objeto ${\displaystyle D_{\mu }}$ tal que

${\displaystyle \phi ^{\dagger }(x)D_{\mu }\phi (x)\rightarrow \phi '^{\dagger }(x)D'_{\mu }\phi '(x)=\phi ^{\dagger }(x)D_{\mu }\phi (x)}$

Electrodinámica cuántica

Si una transformación gauge está dada por

${\displaystyle \psi \mapsto e^{i\Lambda }\psi }$

y para el potencial gauge

${\displaystyle A_{\mu }\mapsto A_{\mu } {1 \over e}(\partial _{\mu }\Lambda )}$

entonces ${\displaystyle D_{\mu }}$ transforma como

${\displaystyle D_{\mu }\mapsto \partial _{\mu }-ieA_{\mu }-i(\partial _{\mu }\Lambda )}$,

y ${\displaystyle D_{\mu }\psi }$ transforma como

${\displaystyle D_{\mu }\psi \mapsto e^{i\Lambda }D_{\mu }\psi }$

y ${\displaystyle {\bar {\psi }}:=\psi ^{\dagger }\gamma ^{0}}$ como

${\displaystyle {\bar {\psi }}\mapsto {\bar {\psi }}e^{-i\Lambda }}$

de modo que

${\displaystyle {\bar {\psi }}D_{\mu }\psi \mapsto {\bar {\psi }}D_{\mu }\psi }$

y ${\displaystyle {\bar {\psi }}D_{\mu }\psi }$ en el lagrangiano de la electrodinámica cuántica es por tanto invariante gauge.

Por otro lado, la derivada no covariante ${\displaystyle \partial _{\mu }}$ no preservaría la simetría gauge del lagrangiano, ya que

${\displaystyle {\bar {\psi }}\partial _{\mu }\psi \mapsto {\bar {\psi }}\partial _{\mu }\psi i{\bar {\psi }}(\partial _{\mu }\Lambda )\psi }$.

Cromodinámica cuántica

En cromodinámica cuántica, la derivada covariante gauge es^[1]​

${\displaystyle D_{\mu }:=\partial _{\mu }-ig\,A_{\mu }^{\alpha }\,\lambda _{\alpha }}$

donde ${\displaystyle g}$ es la constante de acoplamiento, ${\displaystyle A}$ es el campo gauge gluónico, para los ocho gluones diferentes ${\displaystyle \alpha =1\dots 8}$ , ${\displaystyle \psi }$ es un espinor de Dirac de cuatro componentes, y ${\displaystyle \lambda _{\alpha }}$ es una de las ocho matrices de Gell-Mann.

Modelo estándar

La derivada covariante en el Modelo Estándar puede ser expresada en la forma siguiente:^[2]​

${\displaystyle D_{\mu }:=\partial _{\mu }-i{\frac {g_{1}}{2}}\,Y\,B_{\mu }-i{\frac {g_{2}}{2}}\,\sigma _{j}\,W_{\mu }^{j}-i{\frac {g_{3}}{2}}\,\lambda _{\alpha }\,G_{\mu }^{\alpha }}$

donde ${\displaystyle Y}$ es la hipercarga, ${\displaystyle B_{\mu }}$ el bosón gauge del grupo ${\displaystyle U(1)_{Y}}$, ${\displaystyle \sigma _{j}}$ las matrices de Pauli, ${\displaystyle W_{\mu }^{j}}$ los bosones gauge del grupo quiral ${\displaystyle SU(2)_{L}}$ (véase modelo electrodébil), ${\displaystyle \lambda _{\alpha }}$ las matrices de Gell-Mann, ${\displaystyle G_{\mu }^{\alpha }}$ los gluones y ${\displaystyle g_{1}}$, ${\displaystyle g_{2}}$ y ${\displaystyle g_{3}}$ las correspondientes constantes de acoplamiento.

Véase también

• Momento Cinético
• Conexión (matemática)
• Derivada covariante

Referencias